2025年11月4日上午,清华大学科学史系在蒙民伟人文楼B206举办清华科史哲讲座第102讲,由维克多·卡茨(Victor Katz)教授主讲“Musings on Greek Mathematics”。本次讲座由科学史系蒋澈副教授主持。

维克多·卡茨(Victor Katz)教授以“毕达哥拉斯定理”的命名开始了本次讲座,虽然希腊人以“毕达哥拉斯”之名来冠以记录在欧几里得《原本》第一卷第四十七命题,但是“一个直角三角形的两条直角边的平方之和等于斜边的平方”这一定理(Pythagoras Theorem,勾股定理)在世界上其他数学文明中也存在着,且这个名字也没有任何直接历史证据联系到毕达哥拉斯。
卡茨教授继续提出问题,什么叫做希腊数学?首先,希腊数学并不是指是在希腊主流地区(阿提卡大区)成书的数学著作,因为前续提到的毕达哥拉斯大半辈子都居住在西西里半岛。其次,希腊数学也并不是单指用(通用)希腊语写成的数学命题,且不说这门语言一直在变化,西罗马帝国用拉丁语写的数学命题也是我们考量的一部分。以及,那些在莎草纸上和泥石板上写成的数学命题以及那些被亚历山大大帝占领的的地方学习的数学,这些都是希腊数学的一部分:以东地中海地区为主,时间跨度约为公元前400年至公元600年。
接着,卡茨教授以下面两个主要的例子来说明,希腊数学命题在不同的文明/文本记载中的呈现,表明了上述对于泛化的希腊数学定义的支持。
第一个例子是关于正方形对角线的命题,如图一,通用的描述是给出边长和对角线长度,问题是求出正方形的面积或者是给出边长之和,求出对角线长度。现代数学的通用解均利用“和方减差方等于四倍面积”,即,(a+b)² - (a-b)² = 4ab;现有对这一问题的记录在:1)巴比伦证据,现藏于大英博物馆的编号为BM34568的石碑;2)埃及证据,现藏于巴黎的开罗莎草纸(Papyrus Cairo);3)罗马证据,据说是马库斯·朱利叶斯·利奇(Podismus, Marcus Junius Nipsus)的一项工作,他是公元二世纪的罗马测量员;4)现藏于日内瓦的公元二世纪的莎草纸证据。
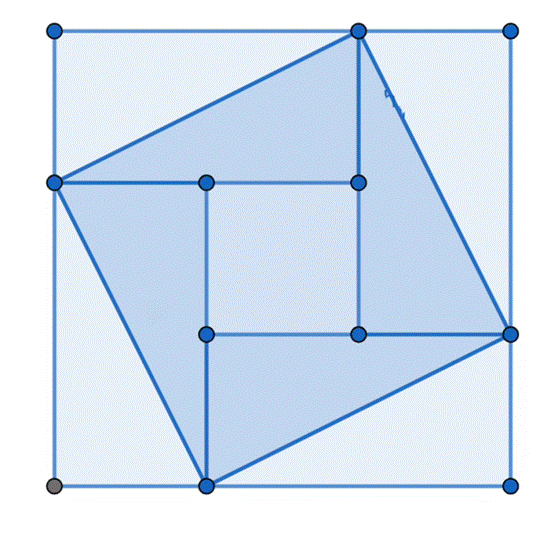
(图片节选自卡茨教授的讲座演示)
上述的对角线问题可以通过移动三角形的位置成为“毕达哥拉斯定理”的证明,同时,这些在不同语言的相似证明说明了几何问题可能通过口头传播流传在东地中海沿岸。需要补充说明的是,汉代赵爽的《周髀算经注》里面也记录了相似的几何证明。
第二个例子是圆弧面积计算问题,首先,生活于公元一世纪亚历山大城的希罗(Hero/Heron)在《度量学》(Metrica)一书中记录了两种圆弧面积的计算方法吗,一种是古代方法,将弦长和圆弧的高相加乘以高的长度再除以二,½(c + h) × h,这种方法只有圆周率为整数3时比较精确;另一种是希罗提到的改进方法,基于阿基米德对于圆周率的精细推算,½(ch) + ¹⁄₁₄(ch)²。希罗提供的是几何里另一种命题形式,它是由问题和解决组成的,与古典意义上的希腊几何的公理演绎结构不同。其次,这样的几何问题也出现在不同的文本中,例如希罗《几何学》(Geometrica)中记载的问题,也能在公元一世纪拉丁农学家科鲁迈拉(Lucius Junius Moderatus Coluomella)的《论农业》中找到,以及在罗马测量员的文集中找到。最后,希罗本人不仅给出了解决特定几何问题的方法,也给出了这些问题解决思路的“算法”或说规则,这是不同于其他实用数学记录的地方。
卡茨教授在最后讨论了希腊数学的“算术”,活跃于公元三世纪的丢番图在《算术》(Arithmetica)中记载的计算问题,和之前的几何问题一样,由一组组具体的问题、解决和规则构成。这些问题也可以在下面讨论中找到:1)十一世纪波斯数学家阿尔-卡拉吉(Al-Karaji)的《法赫里宝典》(Al-Fakhri);2)十三世纪伟大的意大利数学家斐波那契和伊本·班纳·马拉库什(Ibn al-Banna)的讨论中;3)十六世纪犹太学者以利亚·米兹拉希(Elijah Mizrachi)的“旅行问题”。丢番图对于符号/记号的使用也让他的算术问题成为了基础代数问题。
回到毕达哥拉斯,从公元一世纪尼克马库斯(Nichomachus of Gerasa)和五世纪波诶修(Boethius)对于音律比例的讨论中,卡茨教授指出了记载的事实问题,希腊人只是把这些数学命题归功于毕达哥拉斯而已,而这些命题自身是不受语言和地区限制的。最后,卡茨教授引用了维特鲁威 (Vitruvius)《建筑十书》中对于希腊知识的赞扬来结束本场讲座。

在卡茨教授的讲座之后,现场进入了深入的学术研讨环节。与会师生围绕讲座内容,从不同视角出发,提出了一系列富有深度的问题。蒋澈老师首先指出了科鲁迈拉行文中几何问题的表述方式,并对更宏观的希腊数学编史学问题发问。卡茨教授对此作出精辟回应,他指出,尽管“回归语境”已成为当下解读希腊数学的共识,但研究者仍需审慎区分“希腊数学家如何思考”与“希腊数学如何被使用”这两个本质问题。随后,刘钝老师就波斯/阿拉伯数学的传播历史以及“双设法”与卡茨教授探讨细节。廖雨晴同学就欧几里得《原本》中平行公设与“毕达哥拉斯定理”的内在联系提出了一些思考。讨论的广度进一步拓展,潘澍原老师与卡茨教授探讨了中西古代数学文本的留存难题,王哲然老师则继续就讲座细节发问。整场讨论环节丰富、深刻。
撰稿:廖雨晴
审核:蒋澈


